«Понять — значит упростить» — лаконично и точно сформулировали братья Стругацкие в повести “Волны гасят ветер”. Испокон века наука делала именно так.
Ньютон упростил свои законы до одной универсальной идеи — гравитации, объясняющей движения любых тел: от падающих яблок до планет, от полета камня из пращи до пули и ракеты.
Но законы Ньютона, как и вся наука, построенная на их фундаменте, имели пределы. Они не смогли справиться с очень сильной гравитацией, чрезвычайно быстрым движением и сверхмалыми частицами.
Теория относительности и квантовая механика смогли превзойти эти ограничения, по-своему упростив макро и микро-мир парой оригинальных и интригующих идей.
• Гравитация — это искажение пространства-времени массивными телами.
• Свет и элементы, составляющие материю, могут вести себя не только, как частицы, но и как волны.
Но и после триумфа теории относительности и квантовой физика, все равно оставалась область, где наука тщетно пыталась найти способ упростить особый класс систем, не поддававшихся упрощению.
Самое неприятное было в том, что этот неупрощаемый класс т.н. сложных систем встречается буквально повсюду и описывает важнейшие системы мироздания.
• Некоторые из таких систем физические — например, электросети или Интернет.
• Многие из них биологические — мозг, органы, экосистемы.
• Третьи — самый непонятный для упрощения подкласс — социальные системы общества, финансовые рынки, системы корпоративного управления и, конечно же, наше все 21-го века — социальные сети.
И вот, наконец свершилось — смогли упростить и их.
Сознан формализм, позволяющий математически (количественно) описать принципиальное отличие сложных систем от всех остальных классов систем — их структурные свойства, как совокупность отношений между всеми наборами компонентов в системе.
Как измерить сложность.
Четыре года назад Benjamin Allen, Blake C. Stacey and Yaneer Bar-Yam в своей работе "An Information-Theoretic Formalism for Multiscale Structure in Complex Systems" математически описали принципиально новый способ количественного определения структуры и сложности систем.
Системы из разных областей и контекстов могут иметь общие структурные свойства, заставляющие их вести себя одинаково.
По мнению авторов, эти структурные свойства зависят от того, как части системы соединены вместе, и как одни части влияют на действия других.
Стоит дать хотя бы небольшое пояснение связи энтропии и структурных свойств информации.
Энтропия — в широком смысле, означает меру неупорядоченности или хаотичности системы: чем меньше элементы системы подчинены порядку, тем выше энтропия.

Слева целое яйцо (низкая степень беспорядочности = низкая энтропия).
Справа яйцо разбито и все наоборот (высокая степень беспорядочности = высокая энтропия).
Связать энтропию с информацией Шеннон предложил через используемую в статистической физике вероятностную функцию энтропии:

где Pi — это вероятность наступления i-го исхода события;
где i в общем случае принимает значения: i = 1, 2, 3 … N, а в случае текста: i = а, б, в … я.
Получается, что энтропия напрямую связана с «неожиданностью» возникновения события.
Теперь допустим, что некто получил сообщение о том, что из яйца вылупился птенец.
Далее следуют уточнения, что это именно птенец, а не малек, потому что он дышит легкими, а не жабрами, имеет не плавники, а крылья и т. п. Разумеется, все это будет избыточной информацией для получателя, который знает, чем птенец отличается от малька.
Однако та же самая информация, заключенная в генетическом коде,
является именно той структурной информацией, которая определяет весь процесс эмбриогенетического формирования птенца.
Тогда оказывается справедливым, что избыточная информация равна структурной. Из чего следует, что структурная информация равна разнице между максимальной и реальной (наблюдаемой) энтропией (степенью неожиданности), и эта разница может служить количественной мерой упорядоченности текста или структуры любых систем.
Важно отметить, что при исчислении количества информации по
Шеннону игнорируется ее смысл и ее ценность.
Попытки введения количественных мер смысла и ценности информации показали, что эти меры не могут обладать такой же степенью универсальности, как мера, предложенная Шенноном, по той простой причине, что нельзя одними и теми же единицами измерить ценности закона Ома и признания в любви.
Абстрагируясь от смысла и ценности информации, Шеннон фактически поступил так же, как Галилей в свое время поступил с силой трения: исключение этих факторов из поля зрения позволило установить более общий закон.
Мера, найденная Шенноном, оказалась единой универсальной мерой упорядоченности для всех существующих в мире систем.
Однако эта мера, как и законы Ньютона, основывалась на серьёзном упрощении. И потому имела важное ограничение — она не годилась для любых масштабов.
Описание всех этих мер и отношений математически — ключ к царству сложности. Но тут-то и скрывалась проблема: сложные системы слишком сложны для обычных математических подходов.
Можно ожидать, что набор компонентов системы для физических, биологических или социальных объектов реального мира будет настолько сложным, что для всех практических целей их точное описание, в конечном итоге, будет просто неподъемным.
Достижение фундаментального решения этой проблемы имеет решающее значение для нашей способности расширить теоретическую физику, как общий подход к сложным системам, а практическое решение имеет решающее значение для нашей способности решать многие реальные проблемы.
Главная же проблема, с которой здесь столкнулись ученые, была та же, что и для теории относительности и квантовой механики — очень широкий диапазон масштаба систем.

Традиционные информационные меры игнорируют масштаб, в котором проявляется поведение систем. В то же время, системы демонстрируют различное поведение в разных масштабах. Только с учетом важности масштаба можно должным образом учесть структуру и сложность. Эффективный подход требует понимания теории информации в многомасштабном контексте, который не был развит ни в теории информации, ни в статистической физике фазовых переходов.
Авторы новой работы смогли решить эту мега-проблему следующим образом:
• Дано определение структуры как «совокупность отношений между всеми наборами компонентов в системе». Эти отношения определяют, относится ли информация об одной части системы к другим частям системы. Другими словами, структура отражает обмен информацией между частями системы. Обмен информацией означает, — то, что делает одна часть, зависит от того, что делает другая. И этот обмен определяет поведение систем при разных масштабах.
• Вводятся две меры для обобщения понятия структуры систем. Одна из них, называется профилем сложности (он высок для систем, состоящих в основном из независимых частей, и резко падает для сильно взаимозависимых систем). Другая мера называется предельной полезностью информации (она количественно определяет, насколько хорошо система может быть описана с помощью ограниченного объема информации). Вместе эти две меры позволяют избежать многих проблем и парадоксов, которые препятствовали предыдущим подходам к количественной оценке сложности и структуры.
В итоге, данная работа заложила основы нового понимания природы, отличного от простого ее разрезания на кусочки и изучения того, как эти кусочки работают изолированно.
Однако, одним ключём сейф сложных систем не открывался. Четыре года ушло у исследователей на поиск второго ключа к решению задачи формализации сложных систем.
И вот только что опубликованная работа Benjamin Allen, Blake C. Stacey and Yaneer Bar-Yam "The Inherent Instability of Disordered Systems", на основе разработанных ранее количественных мер оценки сложности систем, описывает полный математический формализм развития процесса сложности для систем, находящихся в структурированных средах и имеющих произвольный масштаб.
Любая неструктурированная система, вырастая выше определенного масштаба, не в состоянии противостоять структуре, большей этого масштаба.
Чтобы описать сложную внутреннюю динамику, авторы разработали характеристику многомасштабных изменений в системе. Эта характеристика основана на синтезе кибернетического закона Эшби (Закон необходимого разнообразия — The Law of Requisite Variety) и теоретико-информационных представлений Шеннона о шуме, и при этом учитывает фактор структурирования информации.

Визуально-интуитивная иллюстрация с помощью диаграммы Венна сложности, как функции масштаба шума в системе, состоящей из идеальной подсистемы (голубой цвет) и её зашумленной версии (розовый цвет).
Этот рисунок — трёхмерная визуализация того, как на разных уровнях иерархии работает базовое понятие нового формализма — неприводимые зависимости (irreducible dependencies) между частями (элементами) сложных систем. В отсутствии иерархий (в двумерном варианте) это можно представить с помощью диаграммы Венна следующим образом.
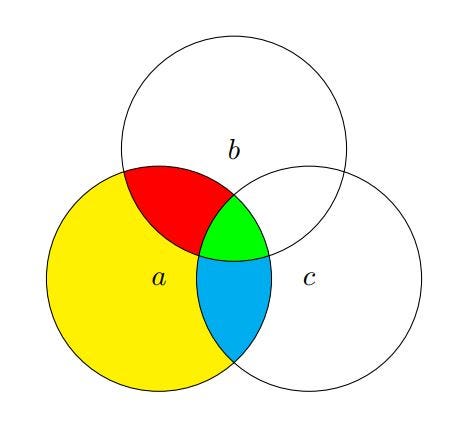
Диаграмма Венна с раскрашенными неприводимыми зависимостями:
- зеленая (a; b; c),
- красная (a; b|c),
- синяя (a; c|b),
- желтая (a|b; c).
Суммируя всю разделяемую информацию для всех покрашенных областей, получаем полную энтропию переменной а. Все другие (приводимые) зависимости — это объединения неприводимых зависимостей. Например, желтая и синяя области комбинируют (a|b), синяя и зеленая вместе дают (a; c), и т.д..
Простота приведенных картинок пусть не ведет к заблуждению, что новый формализм описания сложности систем, на самом деле, не так уж и сложен.
Он весьма сложен и включает в себя 2 леммы и 4 теоремы, выглядящих в виде формул (в качестве примера) так:

Эта теорема показывает, как подсистема становится частью окружающей среды. Из этой теоремы следует, что уровень сложности шума и есть то, что является отличительным свойством отдельных подсистем.
Полученный формализм, в качестве иллюстрации его универсальности, авторы переносят на политический анархизм, показывая, что в обществе спонтанно формируются процессы упорядочения с образованием вышестоящих уровней иерархий, даже при отсутствии традиционных высших иерархий типа правительства.
Выводы этой работы авторы также интерпретируют, как «Обратный второй закон термодинамики» - в то время, как закрытые системы разрушаются до полного беспорядка, системы, открытые для структурированной среды, спонтанно создают порядок на все более высоких уровнях иерархии.
От науки о деградации к науке о самоорганизации.
Согласно автора закона иерархической компенсации Евгения Александровича Седова (в его обобщенной форме, сформулированной А.П. Назаретяном), рост разнообразия на верхнем уровне иерархической организации обеспечивается ограничением разнообразия на предыдущих уровнях, и наоборот — рост разнообразия на нижнем уровне разрушает верхний уровень организации. При этом функциональная унификация несущих структур увеличивает совокупное разнообразие системы.
Иными словами, «иерархические компенсации» — это когда появляется новый лидер эволюции, и старые развивающиеся системы не исчезают, а только меняют свое место в развивающейся системе, в некоторой степени перемещаются на ее периферию и, возможно, становятся несколько сокращенными.
Новый математический формализм, описанный в работе "The Inherent Instability of Disordered Systems", открывает великолепные перспективы, создания законченного формального описания закона иерархической компенсации.
А это, в свою очередь, может стать поворотным моментом в упрощении понимания поведения физических, биологических и социальных систем не только на основе характеристик их составных частей, но и с учетом структуры их взаимодействий.
Возможно также, что этот формализм позволит, выявить соотношение разнообразностных характеристик в системах любого рода — от космофизических до когнитивных — и механизм изменения этого соотношения в процессе эволюции.
Если же принять во внимание, что закон «иерархической компенсации» также является одним из предопределяющих факторов фазовых переходов в процессе общей сингулярности эволюции, то его полная формализация в виде обратного 2-го закона термодинамики может оказаться весьма полезной для перехода от качественных к количественным оценкам.

Зона сингулярности — это практически концентрация кризисов, и мы будем ощущать это время сингулярности как кризисы, которые происходят один за другим, т. е. человечество будет жить на постингулярной стадии, и для каждого кризиса должны быть разработаны компенсационные механизмы.
Важную роль в разработке таких компенсационных механизмов, на мой взгляд, мог бы сыграть формализм обратного 2-го закона термодинамики — возможно, одного из важнейших “упрощений”, необходимых человечеству для понимания бесконечной сложности окружающего нас мира.

Комментариев нет:
Отправить комментарий